ATRACTOR

No artigo De formulis exponentialibus replicatis¹, Euler considera um problema proposto por Condorcet sobre a sucessão $c,c^{c},c^{c^{c}},c^{c^{c^{c}}},...$, sendo $c>0$, convencendo-se, a partir de vários exemplos e alguns cálculos, de que esta sucessão converge se e só se $c\in[e^{-e},e^{\frac{1}{e}}]$. O que é que se passa quando $c>0$ está fora deste intervalo? E se $c$ for complexo?

Por razões que o leitor entenderá em breve, a questão sobre o comportamento assimptótico destas sucessões de exponenciais está relacionada com outra mais simples: Para que valores reais de $a, b > 0$ se tem $a^{b} = b^{a}$? A igualdade é óbvia quando $a = b$. Para valores distintos de $a$ e $b$, podemos listar alguns exemplos simples, como $3^{1}>1^{3},$ $3^{2}>2^{3},$ $3^{2.5}<2.5^{3},$ $3^{4}>4^{3},$ $3^{5}>5^{3},$ $3^{6}>6^{3},$ $2^{1/3}>(1/3)^{2},$ $2^{1}>1^{2},$ $2^{3}<3^{2},$ $2^{4}=4^{2},$ $2^{5}>5^{2},$ $2^{6}>6^{2},$ $(\sqrt{2})^{1/3}>(1/3)^{\sqrt{2}},$ $(\sqrt{2})^{1}>1^{\sqrt{2}},$ $(\sqrt{2})^{2}<2^{\sqrt{2}},$ $(\sqrt{2})^{3}<3^{\sqrt{2}},$ $(\sqrt{2})^{9}>9^{\sqrt{2}}$ mas não se reconhece aqui um padrão geral. Se, porém, reescrevermos a equação $a^{b} = b^{a}$ como $a^{1/a} = b^{1/b}$ e esboçarmos o gráfico da função $x>0\mapsto f(x)=x^{1/x}$, teremos uma ideia aproximada dos valores da imagem de $f$ que são obtidos mais do que uma vez (figura 1).

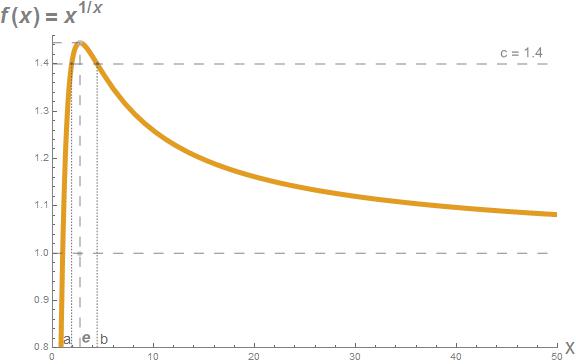
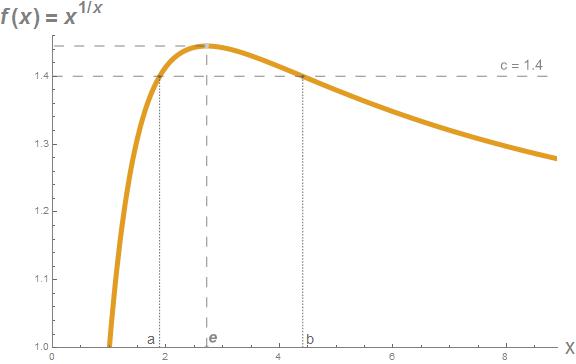
Fig1: Gráficos da função $f$

Página seguinte

(*) Nível de dificuldade: Superior