ATRACTOR

Para que uma estrada permita uma condução suave, deverá preencher, pelo menos, dois requisitos essenciais: que não tenha descontinuidades na sua curvatura e na sua tangência.

A falta de continuidade da sua tangência - que envolve a primeira derivada da função que representa a trajectória de um veículo - encontra-se facilmente em muitas estradas, como se observa, por exemplo, na fotografia abaixo.

Espinho (40º59'39.25''N, 8º38'43.49''W). Imagem retirada de Google Earth.

Esta "curva de 90º" pode aceitar-se numa estrada cujo trânsito circule a baixas velocidades mas nunca, por exemplo, numa auto-estrada. Como é fácil de observar, uma curva deste tipo possui uma variação brusca da tangente no ponto onde os dois segmentos de recta se unem, o que torna impossível transpôr esta curva, em segurança, a grande velocidade.

Veja-se agora a problemática da continuidade da curvatura. Numa estrada formada apenas por segmentos de recta e arcos de circunferência, o valor da curvatura varia bruscamente desde zero (parte recta) até um valor finito e constante (parte circular). Esta descontinuidade da curvatura no ponto de união da parte recta com a parte circular é um problema grave pois, para além de ser bastante incómoda para os condutores e eventuais passageiros, pode ser a causa de acidentes, devido à variação brusca da aceleração centrífuga que se verifica no veículo quando este inicia a sua trajectória circular. Note-se que o valor da aceleração está relacionado com a segunda derivada (tal como acontece com o valor da curvatura).

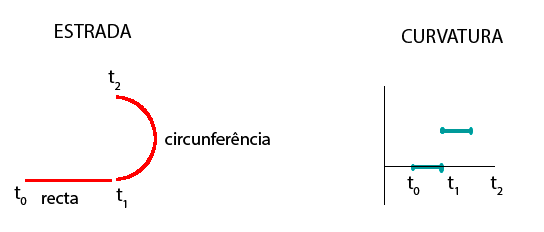
Para evitar este problema, usam-se curvas de transição entre as trajectórias rectas e as trajectórias circulares. Estas curvas terão de ter uma curvatura que varie, gradualmente, desde zero até ao valor da curvatura da circunferência à qual se pretende unir o segmento rectílineo inicial. A curva de transição mais frequente é a clotóide (também designada por espiral de Cornu).

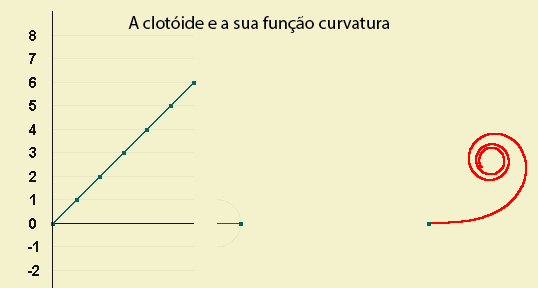
Como se pode observar pelo gráfico, a curvatura da clotóide varia linearmente desde zero até uma qualquer constante e portanto é a curva ideal para ligar um segmento de recta a uma circunferência. Utilizando esta curva, existem várias configurações possíveis que respeitam a continuidade de curvatura, sendo que as mais frequentes são:

1) "recta $\longrightarrow$ clotóide $\longrightarrow$ circunferência"

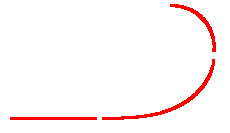
2) "recta $\longrightarrow$ clotóide $\longrightarrow$ circunferência $\longrightarrow$ clotóide $\longrightarrow$ recta"

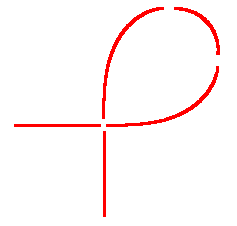
3) "recta $\longrightarrow$ clotóide $\longrightarrow$ clotóide $\longrightarrow$ recta"

Observe as imagens a seguir e verifique se a continuidade de curvatura é preservada em todos os troços de estrada aí representados.

Lisboa (38º45'27.09''N,9º10'19.71''W). Imagem retirada de Google Earth.

Almada (38º39'56.92''N,9º10'18.16''W). Imagem retirada de Google Earth.

Vila Nova de Gaia (41º06'07.99''N,8º34'05.39''W). Imagem retirada de Google Earth.