Analogia

Para explicar a nossa tabela de nós, temos que descrever a noção de nó primo. Isto é feito explicando uma maneira básica de combinar nós.

Trifólio + Figura Oito

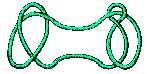
Dados quaisquer dois nós K e L chamamos a este processo de combinação a soma de dois nós e escrevemo-la como K + L .

Houve aqui uma decisão a tomar: se se devia chamar à combinação dos nós «soma» ou «produto». A literatura usa ambos os termos.

Escolhemos o termo soma por duas razões. Uma é que a notação 0 para o lacete sem nó é mais descritiva do que a notação 1.

K + 0 = K

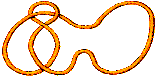
A razão mais importante foi frisar que a analogia não é entre objectos mas entre a maneira como os objectos se comportam, entre as relações entre eles. Portanto, quando fazemos uma analogia entre Trifólio + Figura Oito e 2 x 3 não estamos a dizer que o número 2 é análogo ao Trifólio, mas estamos a dizer que a combinação + de nós tem propriedades análogas ao produto x de números.

Para chamar a atenção para este ponto, é útil ter uma notação diferente para as duas operações que estão a ser consideradas análogas. Usando o termo soma de nós, fazemos uma analogia entre uma soma e uma multiplicação. Esperamos que isto tenha mais impacto e também ilustra um facto geral, que tais analogias podem existir noutras situações.

Embora utilizemos o termo «A aritmética dos nós», também usamos notação algébrica e damos ênfase a leis gerais.

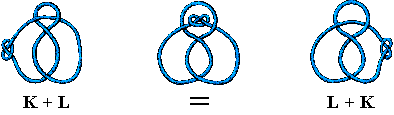
Note aqui que estamos a usar um exemplo particular para ilustrar uma lei geral, a lei comutativa para a soma de nós. Isto ilustra o facto que é como estudo de analogias que a Álgebra obtém a sua generalidade e o seu poder. Quando dizemos que para números m, n temos

estamos a fazer uma analogia entre as propriedades da soma e da multiplicação. Note também que estamos a dar um salto de casos particulares destas leis como

para afirmações gerais, para todos os números.

Ao usar a palavra comum «analogia», estamos a tentar desmitificar e a mostrar que um aspecto do método algébrico é um processo usual pelo qual compreendemos e tentamos extrair ordem do mundo. O outro ponto a frisar é, naturalmente, a excitação de uma analogia inesperada, do «Isto faz-me lembrar ...!».

Conseguimos também ilustrar o facto profundo que os nós têm uma decomposição em soma de nós primos e que esta soma é única «a menos da ordem». Note que esta expressão «a menos da ordem» tem um sentido familiar para um matemático mas não é familiar neste sentido para o público em geral. Foi por isto que demos ilustrações deste facto em vez de uma afirmação geral.

A apreciação desta decomposição levou a que um rapaz perguntasse, após uma Mermaid Molecular Discussion de R.B.: «Há um número infinito de nós primos?». Acontece que a pessoa que fez a palestra não tinha anteriormente formulado a pergunta para ela própria, pelo que teve realmente que pensar para se tornar claro que todos os nós de toro são primos e que há um número infinito de tais nós. Mas a prova de que os nós de toro são primos não é fácil. É bom ter-se algo para expor que seja compreensível e credível mas sem que seja claro como é que se pode demonstrar. Esta é uma das grandes vantagens da teoria dos nós exposta a este nível.